Write My Paper Button

WhatsApp Widget

Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows:

by

Problem 11-11

Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows:

8 questions attached 1

During the next production period, the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $25 for product 1, $28 for product 2, and $30 for product 3.

  1. Formulate a linear programming model for maximizing total profit contribution. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)
    Let Pi = units of product i produced

    Max fill in the blank 1P1 fill in the blank 2P2 fill in the blank 3P3
    s.t.
    fill in the blank 4P1 fill in the blank 5P2 2P3 ≤ fill in the blank 6
    2P1 fill in the blank 7P2 fill in the blank 8P3 ≤ fill in the blank 9
    fill in the blank 10P1 .25P2 fill in the blank 11P3 ≤ fill in the blank 12
    P1, P2, P3 ≥ 0
  3. Solve the linear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution?
    P1 = fill in the blank 13
    P2 = fill in the blank 14
    P3 = fill in the blank 15
    Profit = $  fill in the blank 16
  4. After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had not been taken into account. She noted that setup costs are $400 for product 1, $550 for product 2, and $600 for product 3. If the solution developed in part (b) is to be used, what is the total profit contribution after taking into account the setup costs?
    Profit = $  fill in the blank 17
  5. Management realized that the optimal product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 175 units of product 1, 150 units of product 2, or 140 units of product 3. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300) Here introduce a 0-1 variable yi that is one if any quantity of product i is produced and zero otherwise.
    Max fill in the blank 18P1 fill in the blank 19P2 fill in the blank 20P3 fill in the blank 21y1 fill in the blank 22y2 fill in the blank 23y3
    s.t.
    fill in the blank 24P1 fill in the blank 25P2 2P3 ≤ fill in the blank 26
    2P1 fill in the blank 27P2 fill in the blank 28P3 ≤ fill in the blank 29
    fill in the blank 30P1 .25P2 fill in the blank 31P3 ≤ fill in the blank 32
    fill in the blank 33P1 fill in the blank 34y1 ≤ fill in the blank 35
    fill in the blank 36P2 fill in the blank 37y2 ≤ fill in the blank 38
    fill in the blank 39P3 fill in the blank 40y3 ≤ fill in the blank 41
    P1, P2, P3 ≥ 0; y1, y2, y3 = 0, 1
  7. Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the projected total profit contribution? Compare this profit contribution to that obtained in part (c).
    P1 = fill in the blank 42
    P2 = fill in the blank 43
    P3 = fill in the blank 44
    Profit = $  fill in the blank 45
    The profit is   by $  fill in the blank 47.

Problem 11-13

The Martin-Beck Company operates a plant in St. Louis with an annual capacity of 30,000 units. Product is shipped to regional distribution centers located in Boston, Atlanta, and Houston. Because of an anticipated increase in demand, Martin-Beck plans to increase capacity by constructing a new plant in one or more of the following cities: Detroit, Toledo, Denver, or Kansas City. The estimated annual fixed cost and the annual capacity for the four proposed plants are as follows:

Proposed Plant Annual Fixed Cost Annual Capacity
Detroit $175,000 10,000
Toledo $300,000 20,000
Denver $375,000 30,000
Kansas City $500,000 40,000

The company’s long-range planning group developed forecasts of the anticipated annual demand at the distribution centers as follows:

Distribution Center Annual Demand
Boston 30,000
Atlanta 20,000
Houston 20,000

The shipping cost per unit from each plant to each distribution center is shown in table below.

A network representation of the potential Martin-Beck supply chain is shown in figure below.

Each potential plant location is shown; capacities and demands are shown in thousands of units. This network representation is for a transportation problem with a plant at St. Louis and at all four proposed sites. However, the decision has not yet been made as to which new plant or plants will be constructed.

  1. Formulate a model that could be used for choosing the best plant locations and for determining how much to ship from each plant to each distribution center. There is a policy restriction that a plant must be located either in Detroit or in Toledo, but not both. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)
    Let
    y1 = 1 if a plant is constructed in Detroit; 0 if not
    y2 = 1 if a plant is constructed in Toledo; 0 if not
    y3 = 1 if a plant is constructed in Denver; 0 if not
    y4 = 1 if a plant is constructed in Kansas City; 0 if not
    xij = the units shipped in thousands from plant i to distribution center j
    i= 1,2,3,4,5, and j = 1,2,3
  2. Min fill in the blank 1x11 fill in the blank 2x12 fill in the blank 3x13 fill in the blank 4x21 fill in the blank 5x22 fill in the blank 6x23 fill in the blank 7x31 fill in the blank 8x32 fill in the blank 9x33 fill in the blank 10x41 fill in the blank 11x42
    fill in the blank 12x43 fill in the blank 13x51 fill in the blank 14x52 fill in the blank 15x53 fill in the blank 16y1 fill in the blank 17y2 fill in the blank 18y3 fill in the blank 19y4
s.t.
x11 fill in the blank 21x12 fill in the blank 22x13 fill in the blank 23y1   fill in the blank 25 Detriot capacity
fill in the blank 26x21 fill in the blank 27x22 fill in the blank 28x23 fill in the blank 29y2   fill in the blank 31 Toledo capacity
fill in the blank 32x31 fill in the blank 33x32 fill in the blank 34x33 fill in the blank 35y3   fill in the blank 37 Denver capacity
fill in the blank 38x41 fill in the blank 39x42 fill in the blank 40x43 fill in the blank 41y4   fill in the blank 43 Kansas City capacity
fill in the blank 44x51 fill in the blank 45x52 fill in the blank 46x53   fill in the blank 48 St. Louis capacity
fill in the blank 49x11 fill in the blank 50x21 fill in the blank 51x31 fill in the blank 52x41 fill in the blank 53x51   fill in the blank 55 Boston demand
fill in the blank 56x12 fill in the blank 57x22 fill in the blank 58x32 fill in the blank 59x42 fill in the blank 60x52   fill in the blank 62 Atlanta demand
fill in the blank 63x13 fill in the blank 64x23 fill in the blank 65x33 fill in the blank 66x43 fill in the blank 67x53   fill in the blank 69 Houston demand
xij ≥ for all i and j; y1    , y2    , y3    , y1 + y2    

Formulate a model that could be used for choosing the best plant locations and for determining how much to ship from each plant to each distribution center. There is a policy restriction that no more than two plants can be located in Denver, Kansas City, and St. Louis. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)

Let
y1 = 1 if a plant is constructed in Detroit; 0 if not
y2 = 1 if a plant is constructed in Toledo; 0 if not
y3 = 1 if a plant is constructed in Denver; 0 if not
y4 = 1 if a plant is constructed in Kansas City; 0 if not
xij = the units shipped in thousands from plant i to distribution center j
i= 1,2,3,4,5, and j = 1,2,3
Min fill in the blank 78x11 fill in the blank 79x12 fill in the blank 80x13 fill in the blank 81x21 fill in the blank 82x22 fill in the blank 83x23 fill in the blank 84x31 fill in the blank 85x32 fill in the blank 86x33 fill in the blank 87x41 fill in the blank 88x42
fill in the blank 89x43 fill in the blank 90x51 fill in the blank 91x52 fill in the blank 92x53 fill in the blank 93y1 fill in the blank 94y2 fill in the blank 95y3 fill in the blank 96y4
s.t.
fill in the blank 97x11 fill in the blank 98x12 fill in the blank 99x13 fill in the blank 100y1   fill in the blank 102 Detriot capacity
fill in the blank 103x21 fill in the blank 104x22 fill in the blank 105x23 fill in the blank 106y2   fill in the blank 108 Toledo capacity
fill in the blank 109x31 fill in the blank 110x32 fill in the blank 111x33 fill in the blank 112y3   fill in the blank 114 Denver capacity
fill in the blank 115x41 fill in the blank 116x42 fill in the blank 117x43 fill in the blank 118y4   fill in the blank 120 Kansas City capacity
fill in the blank 121x51 fill in the blank 122x52 fill in the blank 123x53   fill in the blank 125 St. Louis capacity
fill in the blank 126x11 fill in the blank 127x21 fill in the blank 128x31 fill in the blank 129x41 fill in the blank 130x51   fill in the blank 132 Boston demand
fill in the blank 133x12 fill in the blank 134x22 fill in the blank 135x32 fill in the blank 136x42 fill in the blank 137x52   fill in the blank 139 Atlanta demand
fill in the blank 140x13 fill in the blank 141x23 fill in the blank 142x33 fill in the blank 143x43 fill in the blank 144x53   fill in the blank 146 Houston demand
xij ≥ for all i and j; y1    , y2    , y3    , y3 + y4    

Problem 11-3

Consider the following all-integer linear program:

  1. Choose the correct graph which shows the constraints for this problem and uses dots to indicate all feasible integer solutions.

(i) 8 questions attached 2 (ii) 8 questions attached 3
(iii) 8 questions attached 4 (iv) 8 questions attached 5

Graph_______?_______
 

  1. Solve the LP Relaxation of this problem.
    The optimal solution to the LP Relaxation is x1 = fill in the blank 2, x2 = fill in the blank 3. Its value is fill in the blank 4.
  2. Find the optimal integer solution.
    The optimal solution to the LP Relaxation is x1 = fill in the blank 5, x2 = fill in the blank 6. Its value is fill in the blank 7.

Problem 11-23

Roedel Electronics produces a variety of electrical components, including a remote control for televisions and a remote control for DVD players. Each remote control consists of three subassemblies that are manufactured by Roedel: a base, a cartridge, and a keypad. Both remote controls use the same base subassembly, but different cartridge and keypad subassemblies.

Roedel’s sales forecast indicates that 7000 TV remote controls and 5000 DVD remote controls will be needed to satisfy demand during the upcoming Christmas season. Because only 500 hours of in-house manufacturing time are available, Roedel is considering purchasing some, or all, of the subassemblies from outside suppliers. If Roedel manufactures a subassembly in-house, it incurs a fixed setup cost as well as a variable manufacturing cost. The following table shows the setup cost, the manufacturing time per subassembly, the manufacturing cost per subassembly, and the cost to purchase each of the subassemblies from an outside supplier:

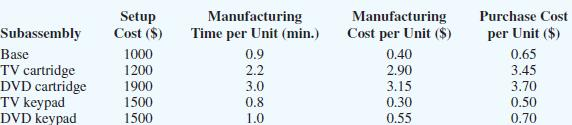
8 questions attached 6

  1. Determine how many units of each subassembly Roedel should manufacture and how many units Roedel should purchase.
    Variable names Value
    No. of bases manufactured fill in the blank 1
    No. of bases purchased fill in the blank 2
    No. of TV cartridges made fill in the blank 3
    No. of TV cartridges purchased fill in the blank 4
    No. of DVD cartridge made fill in the blank 5
    No. of DVD cartridge purchased fill in the blank 6
    No. of TV keypads made fill in the blank 7
    No. of TV keypads purchased fill in the blank 8
    No. of DVD keypads made fill in the blank 9
    No. of DVD keypads purchased fill in the blank 10
  2. What is the total manufacturing and purchase cost associated with your recommendation?
    $  fill in the blank 11
  3. Suppose Roedel is considering purchasing new machinery to produce DVD cartridges. For the new machinery, the setup cost is $3000; the manufacturing time is 2.5 minutes per cartridge, and the manufacturing cost is $2.60 per cartridge. Assuming that the new machinery is purchased, determine how many units of each subassembly Roedel should manufacture and how many units of each subassembly Roedel should purchase.
    Variable names Value
    No. of bases manufactured fill in the blank 12
    No. of bases purchased fill in the blank 13
    No. of TV cartridges made fill in the blank 14
    No. of TV cartridges purchased fill in the blank 15
    No. of DVD cartridge made fill in the blank 16
    No. of DVD cartridge purchased fill in the blank 17
    No. of TV keypads made fill in the blank 18
    No. of TV keypads purchased fill in the blank 19
    No. of DVD keypads made fill in the blank 20
    No. of DVD keypads purchased fill in the blank 21
  4. What is the total manufacturing and purchase cost associated with your recommendation?
    $  fill in the blank 22
    Do you think the new machinery should be purchased?
     
    Explain.
    The input in the box below will not be graded, but may be reviewed and considered by your instructor.

Problem 11-1

(a) Indicate whether the following linear program is an all-integer linear program or a mixed-integer linear program.
Max 30x1 + 25x2
s.t.
3x1 + 1.5x2 ≤ 400
1.5x1 + 2x2 ≤ 250
1x1 + 1x2 ≤ 150
x1, x2 ≥ 0 and x2 integer
This is a  ____?_____linear program.
Write the LP Relaxation for the problem but do not attempt to solve.
If required, round your answers to one decimal place.
Its LP Relaxation is
Max fill in the blank 2x1 + _______?_____x2
s.t.
fill in the blank 4x1 + 1.5x2  __?___
1.5x1 + fill in the blank 7x2   _____?____
fill in the blank 10x1 + ___?____x2   ____?____
x1 , x2    
(b) Indicate whether the following linear program is an all-integer linear program or a mixed-integer linear program.
Max 3x1 + 4x2
s.t.
2x1 + 4x2 ≥ 8>
2x1 + 6x2 ≥ 12
x1, x2 ≥ 0 and integer
This is a   linear program.
Write the LP Relaxation for the problem but do not attempt to solve.
If required, round your answers to one decimal place.
Its LP Relaxation is
Max fill in the blank 17x1 + fill in the blank 18x2
s.t.
2x1 + fill in the blank 19x2   fill in the blank 21
fill in the blank 22x1 + 6x2   fill in the blank 24
x1 , x2    

Problem 12-07

Hanson Inn is a 96-room hotel located near the airport and convention center in Louisville, Kentucky. When a convention or a special event is in town, Hanson increases its normal room rates and takes reservations based on a revenue management system. The Classic Corvette Owners Association scheduled its annual convention in Louisville for the first weekend in June. Hanson Inn agreed to make at least 50% of its rooms available for convention attendees at a special convention rate in order to be listed as a recommended hotel for the convention. Although the majority of attendees at the annual meeting typically request a Friday and Saturday two-night package, some attendees may select a Friday night only or a Saturday night only reservation. Customers not attending the convention may also request a Friday and Saturday two-night package, or make a Friday night only or Saturday night only reservation. Thus, six types of reservations are possible: convention customers/two-night package; convention customers/Friday night only; convention customers/Saturday night only; regular customers/two-night package; regular customers/Friday night only; and regular customers/Saturday night only.

The cost for each type of reservation is shown here.

8 questions attached 7

The anticipated demand for each type of reservation is as follows:

8 questions attached 8

Hanson Inn would like to determine how many rooms to make available for each type of reservation in order to maximize total revenue.

  1. Define the decision variables and state the objective function.
    Let CT = number of convention two-night rooms
    CF = number of convention Friday only rooms
    CS = number of convention Saturday only rooms
    RT = number of regular two-night rooms
    RF = number of regular Friday only rooms
    RS = number of regular Saturday only room
  2.   fill in the blank 2CT fill in the blank 3CF fill in the blank 4CS fill in the blank 5RT fill in the blank 6RF fill in the blank 7RS
  4. Formulate a linear programming model for this revenue management application.
      fill in the blank 9CT fill in the blank 10CF fill in the blank 11CS fill in the blank 12RT fill in the blank 13RF fill in the blank 14RS
  5. S.T.
  6. 1) fill in the blank 15CT   fill in the blank 17
    2) fill in the blank 18CF   fill in the blank 20
    3) fill in the blank 21CS   fill in the blank 23
    4) fill in the blank 24RT   fill in the blank 26
    5) fill in the blank 27RF   fill in the blank 29
    6) fill in the blank 30RS   fill in the blank 32
    7) fill in the blank 33CT fill in the blank 34CF   fill in the blank 36
    8) fill in the blank 37CT fill in the blank 38CS   fill in the blank 40
    9) fill in the blank 41CT fill in the blank 42CF fill in the blank 43RT fill in the blank 44RF   fill in the blank 46
    10) fill in the blank 47CT fill in the blank 48CS fill in the blank 49RT fill in the blank 50RS   fill in the blank 52
  8. What is the optimal allocation and the anticipated total revenue?
    Variable Value
    CT fill in the blank 53
    CF fill in the blank 54
    CS fill in the blank 55
    RT fill in the blank 56
    RF fill in the blank 57
    RS fill in the blank 58
  9. Total Revenue = $  fill in the blank 59
  10. Suppose that one week before the convention, the number of regular customers/Saturday night only rooms that were made available sell out. If another nonconvention customer calls and requests a Saturday only room, what is the value of accepting this additional reservation?
    The shadow price for constraint 10 is $  fill in the blank 60 and shows an added profit of $  fill in the blank 61 if this additional reservation is accepted.

Problem 12-11 (Algorithmic)

Consider the problem

Min 2X2 – 15X + 2XY + Y2 – 20Y + 65
s.t. X + 3Y ≤ 10
  1. Find the minimum solution to this problem. If required, round your answers to two decimal places.
    The optimal solution is X = fill in the blank 1, Y = fill in the blank 2, for an optimal solution value of fill in the blank 3.
  2. If the right-hand side of the constraint is increased from 10 to 11, how much do you expect the objective function to change? If required, round your answer to two decimal places.
    The optimal objective function value will   by fill in the blank 5.
  3. Re-solve the problem with a new right-hand side of 11. How does the actual change compare with your estimate? If required, round your answers to two decimal places.
    The new optimal objective function value is fill in the blank 6 so the actual   is fill in the blank 8.

Problem 12-23

Markowitz portfolio optimization: Harry Markowitz received the 1990 Nobel Prize for his path-breaking work in portfolio optimization. One version of the Markowitz model is based on minimizing the variance of the portfolio subject to a constraint on return. The below table shows the annual return (%) for five 1-year periods for the six mutual funds with the last row that gives the S&P 500 return for each planning scenario. Scenario 1 represents a year in which the annual returns are good for all the mutual funds. Scenario 2 is also a good year for most of the mutual funds. But scenario 3 is a bad year for the small-cap value fund; scenario 4 is a bad year for the intermediate-term bond fund; and scenario 5 is a bad year for four of the six mutual funds.

8 questions attached 9

If each of the scenarios is equally likely and occurs with probability 1/5, then the mean return or expected return of the portfolio is

8 questions attached 10

Using the scenario return data given in Table above, the Markowitz mean-variance model can be formulated. The objective function is the variance of the portfolio and should be minimized. Assume that the required return on the portfolio is 10%. There is also a unity constraint that all of the money must be invested in mutual funds.

Most investors are happy when their returns are “above average,” but not so happy when they are “below average.” In the Markowitz portfolio optimization model given above, the objective function is to minimize variance, which is given by

where Rs is the portfolio return under scenario s and R is the expected or average return of the portfolio.

With this objective function, we are choosing a portfolio that minimizes deviations both above and below the average, R. However, most investors are happy when Rs > R, but unhappy when Rs < R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below R.

Let Dsp – Dsn – Rs – R and restrict Dsp and DDsn to be nonnegative. Then Dsp measures the positive deviation from the mean return in scenario s (i.e., DDsp = Rs – R when Rs R)

In the case where the scenario return is below the average return, Rs < R, we have – Dsn = Rs – R. Using these new variables, we can reformulate the Markowitz model to only minimize the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.

Solve the Markowitz portfolio optimization model that can be prepared for above case to use semivariance in the objective function. Solve the model using either Excel Solver or LINGO. If required, round your answers to one decimal place.

Mutual Funds Investments in %
Foreign Stock fill in the blank 1%
Intermediate-Term Bond fill in the blank 2%
Large-Cap Growth fill in the blank 3%
Large-Cap Value fill in the blank 4%
Small-Cap Growth fill in the blank 5%
Small-Cap Value fill in the blank 6%
Don`t copy text!
WeCreativez WhatsApp Support
Our customer support team is here to answer your questions. Ask us anything!
???? Hi, how can I help?
Hi, how can I help?