Assignment ID: FG133083460
Question 1: Prove that a set A is finite exactly when each non-empty subset of P (A) has a maximum element regarding ⊆
Question 2: Let x be a set. Then x is an ordinal exactly then, when each personal transitive subset of x is an element of x.
Question 3: Let Φ(x) be a set-theoretic property. We will be saying that Φ is transitive on the ordinals if:(∀α)(∀β)[α ∈ β => Φ(β) => Φ(α)] . Prove that if Φ is transitive on the ordinals, then:
For every ordinal α, for which ¬Φ(α) then (∀β)[Φ(β) ⇒ β < α];
If the set A, where (∀α)[α ∈ A ⇐⇒ Φ(α)], does not exist, then ∀α(Φ(α)).
Question 4: Let A be an infinite set. Prove that if there is a good ordinance ≤1 in A, then there is a good ordinance ≤2 in A, for which the well-ordered sets {A, ≤1} and {A, ≤2} are not isomorphic.
Question 5: Prove that in {P (ω), ⊆} there are chains that are equivalent to P (ω).
Question 6: Let X ⊆ R be well ordered by the usual ordinance in R. Prove that X is either finite or countable.
Question 7: Prove that for any set A the following are valid:
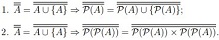
WE ALL KNOW CLASSWORK IS BORING. RELY ON OUR PROFESSIONAL TUTORS TO HELP YOU WITH ALL YOUR CLASS WORK ESSAYS & ASSIGNMENTS. ORDER YOUR CUSTOM PAPER FOR 15% DISCOUNT. USE CODE SAVE15

The post Prove that a set A is finite » Full Grade appeared first on Cheap Accounting Tutors.