1. Compute the area of the region outside the circle r = 3 and outside
the cardioid r = 2(1 + cos(θ)).
2. (a) Please kindly find the length of the curve defined by the expression
r(θ) = k sec(θ), θ ∈ [0, β]; k is a constant. (b) Sketch the curve for k = 1 and β = π/3.
3. In polar coordinates the position of a point-particle is described by the
vector ~r = rrˆ(θ), where r = r(t) is the radial coordinate, rˆ(θ) is a unit vector in the radial direction, θ = θ(t). The parameter t represents time. Knowing that
(d/ dθ) rˆ= θ ˆ, (d/dθ)θˆ = −r ˆ, where θˆ is a unit vector in the angular direction, use the chain rule to show that the velocity and acceleration vectors are, respectively,
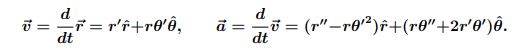
Notation: the prime denotes a derivative with respect to time.
Remark: vr = r′ is the tangencial velocity; vθ = rθ′ is the angular velocity; aθ = rθ′2 is the centripetal acceleration; ac = 2r′θ′ is the coriolis acceleration.
Take professional academic assistance & Get 100% Plagiarism free papers
Chat Now
4. The ideal gas equation for one mol reads P V = RT, where the universal gas constant is R = 8.314 J/mol/K. Find the rate at which the pressure P of the gas is changing when its volume V is 20 L and is increasing at a rate of 0.2 L/s, and its temperature T is 300 K and is increasing at a rate of 0.3 K/s. Dimensions: J=Joules, K=Kelvins, L=Litres, s=seconds. The pressure comes in Pascals.
Hint: Set P = P (V, T ) where both V and T depend on time; apply the chain rule to find the rate dP/dt, t: time.
5. The height of a hill (in feet) is given by h(x, y) = 20(16 − 4x²− 3y²+ 2xy + 28x − 18y); x denotes the distance (in miles) east and y stands for the distance (in miles) north of Bolton City. In what direction is the slope of the hill steepest at a point 1 mile north and 1 mile east of Bolton? What is the steepest slope at that point?
6. The simplest dispersive wave equation is ut + ux + uxxx = 0, u ≡ u(x, t). Show that the harmonic function u(x, t) = B sin(kx − ωt) is a solution of the above differential equation if ω = k−k³, the dispersion relation.
The post Compute the Area of the Region Outside the Circle r = 3 and Outside the Cardioid: Multivariable Calculus Assignment, CU, Canada appeared first on .

